Multiplication of Square Matrices

When multiplying 2 matrices we need to consider the dimensions of each, as multiplication is not possible if the dimensions are not aligned appropriately.

The easiest multiplication to consider is that of two square matrices of the same dimensions n x n .

A square matrix is a matrix that has the same number of rows and columns.

The matrix below is a square matrix of m x m . It has m rows and m columns.

A=\begin{bmatrix} a_{11} &a_{12} &a_{13}&..& a_{1m}\\ a_{21} &a_{22} &a_{23}&..& a_{2m}\\a_{31} &a_{32} &a_{33}&..& a_{3m}\\ :\\a_{m1} &a_{m2} &a_{m3}&……& a_{mm}\end{bmatrix}

Equation 14

Matrix A in Equation 14 can be multiplied with other square matrices of the same dimension , m x m .

The result will be a new square matrix of the same dimensions.

The easiest way to demonstrate the actual multiplication is with an example:

Let P and Q be two square matrices of 3 x 3 .

P=\begin{bmatrix} p_{11} &p_{12} &p_{13}\\ p_{21} &p_{22} &p_{23}\\p_{31} &p_{32} &p_{33}\end{bmatrix}

Q=\begin{bmatrix} q_{11} &q_{12} &q_{13}\\ q_{21} &q_{22} &q_{23}\\q_{31} &q_{32} &q_{33}\end{bmatrix}

To multiply P by Q we need to do the following:

P x Q = \begin{bmatrix} p_{11}q_{11}+p_{12}q_{21}+p_{13}q_{31} &p_{11}q_{12}+p_{12}q_{22}+p_{13}q_{32} &p_{11}q_{13}+p_{12}q_{23}+p_{13}q_{33} \\ p_{21}q_{11}+p_{22}q_{21}+p_{23}q_{31} &p_{21}q_{12}+p_{22}q_{22}+p_{23}q_{32} &p_{21}q_{13}+p_{22}q_{23}+p_{23}q_{33} \\ p_{31}q_{11}+p_{32}q_{21}+p_{33}q_{31} &p_{31}q_{12}+p_{32}q_{22}+p_{33}q_{32} &p_{31}q_{13}+p_{32}q_{23}+p_{33}q_{33} \end{bmatrix}

Equation 15

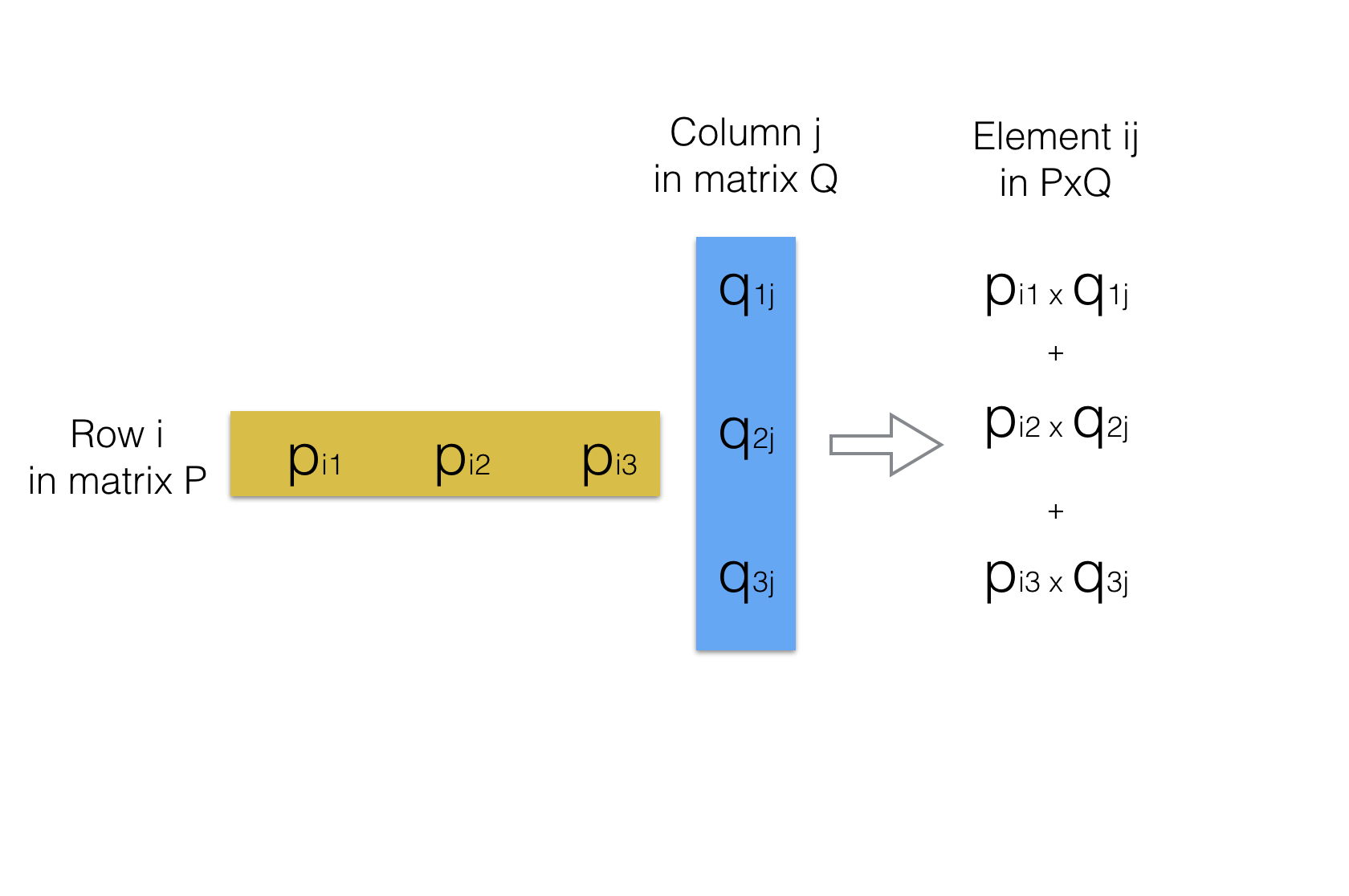
Notice the pattern of finding each element in the multiplication result.

Each element ij in P x Q is a result of multiplying all elements in row i of matrix P with the corresponding j elements in column j of matrix Q .

See the picture below for an illustration :

if A is an n × m matrix and B is an m × p matrix, their matrix product AB is an n × p matrix, in which the m entries across a row of A are multiplied with the m entries down a column of B and summed to produce an entry of AB. When two linear transformations are represented by matrices, then the matrix product represents the composition of the two transformations.